Компартментна модель, яка описує динаміку водного режиму ґрунту, багато в чому аналогічна моделі теплоперенесення. Маються, однак, і принципові розходження. Перше з них пов'язано з тим, що вхідні в модель коефіцієнти самі залежать від моделюємої величини – вологості ґрунту або водного потенціалу. Тим самим моделі стають нелінійними, що різко ускладнює як аналіз, так і чисельне рішення рівнянь переносу. Друга відмінність пов'язана з тим, що в кожному компартменті з'являється функція внутрішнього стоку – поглинання води коренями. Тим самим задача кількісного опису динаміки вологообміну стає більш складною. З'являється необхідність зв'язати її з процесами, які відбуваються в інших блоках моделі не тільки через граничну умову (умова на границі ґрунт – повітря), але і через функцію розподілених по ґрунтовому профілю стоків, їхній сумарний транспорт по рослині і транспірацію.

         Розглянемо рівняння водного балансу у деякому ґрунтовому шарі. За аналогією з (3.52) зміну вологовмісту у j-му компартменті за малий проміжок часу Dt = t_k+1 – t_k можна записати у вигляді

       DW_j = W_j (t_k+1) – W_j (t_k) = [(v_j+l – v_j) – h_j f_j] FDt,                            (9.38)

 

F і h_j – відповідно площа і товщина компартмента;

v_j і v_j+1 – швидкість руху води через верхню і нижню границі;

f_j – швидкість поглинання води коренями, яка віднесена до одиниці об'єму ґрунту.

Співвідношення (9.38) є не що інше, як рівняння балансу (або нерозривності): кількість рідини, яка поступає в компартмент дорівнює  v_j+1FDt, а яка витікає дорівнює сумі потоку через нижню межу  v_jDt і кореневого поглинання  f_j h_j FDt.

Рівняння для швидкості руху води записано вище . Використовуючи аналогію температури з водним потенціалом і вологопровідності з теплопровідністю,  запишемо

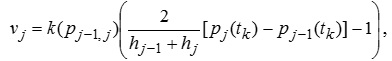          ,                           (9.40)

і

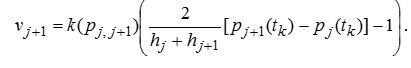                .                            (9.41)

 

        Тим самим отримано зв'язок приросту вологовмісту компартмента за один часовий крок моделі з водним потенціалом даного компартмента  р_j(t_k)  і двох сусідніх   p_j–1(t_k)  і  p_j+1(t_k) на початку цього кроку.

        Для проведення розрахунків динаміки руху вологи необхідно, таким чином, використовувати залежність потенціалу від вологості. Ця залежність саме і визначається ОГХ. Використання ОГХ дозволяє виключити одну з двох цих величин і записати рівняння або для динаміки вологовмісту, або для динаміки водного потенціалу. Звичайно перевагу має другий шлях, для чого приводяться два аргументи. Перший з них зводиться до того, що поглинання вологи коренями визначається різницею водяних потенціалів ґрунту і рослини і для замикання моделі все рівно приходиться розраховувати потенціали. Другий заснований на аналогії: рівняння теплоперенесення записані для аналога потенціалу – температури, а не для аналога вологості – кількості потенціалу в компартменті. Якщо продовжити цю аналогію, то цілком природним буде введення «диференціальної вологоємності» ґрунту як коефіцієнта  , який пов'язує збільшення вологості зі збільшенням потенціалу.

  .                                                                   (9.42)

 

Вона показує, наскільки змінюється вологість ґрунту при зміні її водного потенціалу на одиницю. На відміну від теплоємності диференціальна вологоємність ґрунту непостійна. Вона залежить від потенціалу, оскільки це не що інше, як похідна водоутримуваної здатності ґрунтів, побудованої в координатах: р – вісь абсцис, w – вісь ординат. Таким чином, m=m(р).

         Використовуючи введене тут поняття диференціальної вологоємності і, приймаючи до уваги, що вологозапас компартмента W_j дорівнює його об'єму h_jF, помноженому на вологість w_j, запишемо рівняння балансу замість (9.38) у наступному вигляді

 

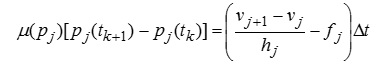                .               (9.43)

 

 

Це співвідношення створює разом з (9.42) і (9.43) замкнуту систему рівнянь для розрахунку водного потенціалу ґрунту «крок за кроком».

          На межі ґрунт – повітря має бути заданий потік вологи – негативний у випадку випадання опадів і позитивний – при випаровуванні. При цьому інтенсивні дощі приводять до того, що волога не встигає усмоктуватися верхнім шаром ґрунту і просочується в глиб ґрунтового профілю. При наявності схилу це приводить до стікання частини води, а на горизонтальних ділянках і нерівностях поля утворяться калюжі. У моделі шар вільної вологи на поверхні ґрунту рівномірно «розповсюджується» по всьому полю і характеризується наведеною висотою стовпа води, що досягає декількох міліметрів. Ця величина додається до водного потенціалу, який при наявності насиченого вологою верхнього шару стає позитивним.

            Після припинення опадів вільна волога частково випаровується, а частково усмоктується в ґрунт. При цьому «працює» саме криволінійна ділянка ОГХ, близька до вертикалі. Ця обставина ускладнює процес розрахунку і приводить до того, що в досить докладних моделях режим усмоктування повинен описуватися за допомогою спеціальних алгоритмів. У прикладних моделях, де не потрібна висока точність, ці труднощі обходяться за рахунок використання дещо спрощеного перерозподілу надлишкової вологи по ґрунтових компартментах. Цей процес починається з верхнього компартмента, який заповнюється до ПВ чи НВ, якщо залишилися волога то додається у другий компартмент і т.д. – доти, поки запас надлишкової вологи не буде вичерпаний. Якщо при цьому виявляється, що весь ґрунтовий профіль насичений водою, вважається, що надлишкова кількість вологи виноситься за межі розрахункового шару.

           Розглянемо тепер особливості врахування кореневого поглинання. Врахування впливу коренів у моделі проводиться шляхом завдання об'ємної щільності їхньої поглинаючої поверхні. Виділимо на деякій глибині одиничний об'єм ґрунту. Якщо після відмивання всіх живих коренів у цьому об'ємі виміряти площу їхньої поверхні і розділити на об'єм, то саме й отримаємо цю величину, яку будемо позначати через w. Величина w залежить від глибини х і змінюється з часом у зв'язку з ростом рослин і розвитком кореневої системи, тобто

 

 

                             w = w(х, t).                                                         (9.44)

 

Вона вимірюється в см²/см³, тобто в см^–1. Очевидно, що поза зоною проникнення коренів w(х, t) = 0. Будемо вважати, що об'ємна щільність коренів постійна всередині кожного компартмента. Тоді для функції стоку води у корінь у j-му компартменті, вираженій в см³/год. або в см³/доба, можна записати:

                            f_j =w_j x(p_j–P_r),                                                              (9.45)

 

де Р_r – водний потенціал кореня, a x – його провідність.

           При цьому стінки провідних судин кореня від епідерміса до ксилеми мають найбільший опір. По провідних судинах ксилеми вода рухається майже без опору, в зв'язку з чим водний потенціал усієї кореневої системи можна вважати постійним, поза залежністю від глибини шару або від номера компартмента. Таким чином, для розрахунку динаміки ґрунтової вологи необхідно знати додатково значення об'ємної площі кореня в компартментах w, провідність кореня x і його водний потенціал Р_r.

Помножимо вираз (9.45) на товщину компартмента h_j і візьмемо суму всіх цих рівностей, починаючи з одиниці і, кінчаючи NR — номером компартмента, у якому ще містяться корені:

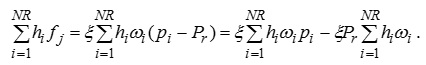            .                     (9.46)

 

У виразі (3.71) остання сума безрозмірна і представляє собою площу коренів, віднесену до одиниці площі поля. За аналогією з листковим індексом її можна назвати «кореневим індексом» і позначити через W:

 

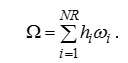                .                                                                    (9.47)

 

Ліва частина виразу (9.47) є не що інше, як сумарне поглинання води коренями. Тому, якщо знехтувати акумуляцією води тканинами рослин, можна прирівняти його до транспірації

 

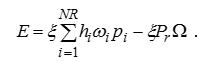                         .                                             (9.48)

 

Звідси можна виразити потенціал кореня Рr через транспірацію

 

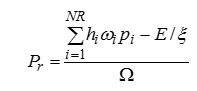                                                            (9.49)

 

і для поглинання води коренями у j-му компартменті (9.49) записати

 

 

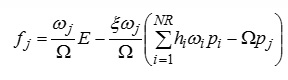                     .                          (9.50)

 

      

 Приймається, що водний потенціал безпосередньо поблизу кореня дорівнює його середньому значенню на даній глибині ґрунтового профілю.

Розглянемо два окремих випадки, у яких рівняння для опису процесу поглинання води коренями спрощується.

         1. При високій вологості ґрунту pi » 0 або в більш загальному випадку рi постійне по всьому ґрунтовому профілю. У такому випадку замість (9.50) отримаємо

 

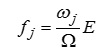                                        .                                                         (9.51)

 

          2. В іншому випадку, коли корені розподілені по всьому ґрунтовому профілю рівномірно (що має місце, наприклад, у вегетаційних судинах), wi  не залежить від номера i,   W = wh_r  i

 

                                          f_j = E/h_r ,                                                        (9.52)

 

 

де h_r – глибина проникнення коренів.

        Очевидно, що перший додаток у (9.50) є, таким чином, визначальним. Роль другого зводиться до врахування нерівномірності розподілу коренів або нерівномірного розподілу водного потенціалу по всій глибині ґрунту.

          Завершуючи розгляд компартментаної моделі вологообміну, випишемо основні рівняння для того випадку, коли всі компартменти мають однакові висоти, h_j = h.

Рівняння балансу ґрунтової вологи у j-му компартменті має вигляд

 

 

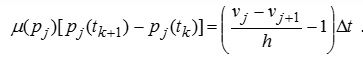              .                           (9.53)

 

 

Для швидкостей руху води із сисних компартментів отримаємо

 

 

  ,

 

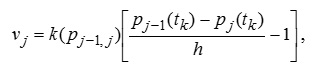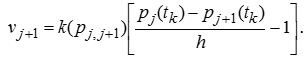  .                       (9.54)

 

         Ці співвідношення справедливі для всіх компартментів, крім нульового й останнього. Тому до них необхідно додати граничні умови. Якщо, наприклад, нижня межа відповідає рівню залягання грунтових вод, то нижня гранична умова має вигляд

                                      p_NS = 0.                                                                       (9.55)

 

На верхній межі при розрахунку режиму висушування додається умова заданого потоку – так названого фізичного випаровування. При цьому, рівняння балансу вологи у нульовому компартменті записується у вигляді:

    ,          (9.56)

 

де фізичне випаровування Еs повинне задаватися або обчислюватися c залученням додаткових міркувань. Використовуючи наведені вище рівняння при заданні початкового розподілу вологи wj (або потенціалу) по компартментах, параметрів рослини x, w_j і W,

випаровування Es і транспірації Er можна розраховувати зміни профілю водного потенціалу і, отже, вологості ґрунту крок за кроком, подібно тому, як це робиться при розрахунку теплоперенесення.

       Зміна вологості ґрунту за період вегетації. На земну поверхню випадає протягом року в середньому 710 мм опадів, а сумарне випаровування складає 240 мм, проте, розподіл опадів, як по територіях областей, так і в кожному місці протягом року нерівномірний і ґрунтова волога в багатьох випадках є фактором, який лімітує урожай. Більш того, багато регіонів нашої країни періодично страждають від посухи, так що прогноз водного режиму ґрунтів і раціональне використання водних ресурсів є в землеробстві одним з найважливіших. При моделюванні водного режиму варто звернути увагу на два моменти – це по-перше, динаміка продуктивної вологи, найчастіше, у метровому шарі ґрунту і, по-друге, розподіл вологозапасів по ґрунтовому профілі.

Вологість ґрунту не має чітко вираженого добового ходу. Добовим коливанням піддається транспірація, тобто швидкість вилучення води з ґрунту за режиму висушування. Однак ці коливання мало відбиваються на загальному балансі. Вологозапаси у ґрунті досить швидко збільшуються при випаданні опадів і при поливах, а в проміжках між опадами й у міжполивні періоди повільно зменшуються. Це зменшення частково відбувається за рахунок гравітаційного стікання води, але в більшості за рахунок транспірації і поверхневого випаровування. Тому типовий сезонний хід вологозапасів має чітко виражений пилкоподібний характер. При цьому в залежності від балансу опадів і транспірації вологість ґрунту в середньому за досить тривалі періоди (декада, місяць) або збільшується, або зменшується.

Типовою є ситуація, коли рослини у перший період свого життя забезпечуються водою за рахунок весняних запасів вологи, які утворилися в результаті випадання осінніх дощів і танення снігу. Надалі доля посіву залежить від поповнення вологи, оскільки інтенсивна транспірація, починаючи з моменту виходу в трубку, приводить до швидкого витрачання запасеної вологи. У цьому процесі істотну роль грає вертикальний розподіл ґрунтової вологи. Оскільки висушування починається з верхніх шарів ґрунту, то доля урожаю багато в чому залежить від того, наскільки швидко корені рослин проникають у більш глибокі ґрунтові шари, де вони можуть знайти достатню кількість вологи. При цьому особливу роль починають грати адаптивні властивості рослин, які приводять до прискореного росту коренів у глиб ґрунту при водному дефіциті.

             Для ілюстрації цього феномена на рис.9.12 представлена схематична картина зміни поглинання води коренями протягом вегетації, а на рис. 3.20 показана зміна профілю ґрунтової вологи також за тривалий період часу. Якщо ці два процеси – ріст корінняенів і висушування ґрунту – узгоджені, то рослини можуть і не зазнавати глибокого водного стресу, незважаючи на зменшення сумарних вологозапасів у метровому шарі ґрунту. Правда, при цьому виникає питання про «неузгодженість» профілів доступної вологи і доступних форм елементів живлення. Але це вже більш складне питання, до розгляду якого ми ще повернемося.

 

   

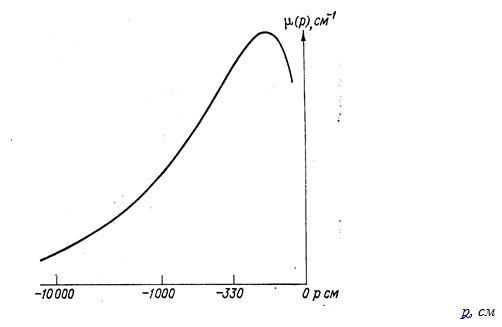
   Рис.9.12. Диференціальна вологоємність ґрунту.

 

 

 Таблиця 9.5 – Деякі напівемпіричні моделі ОГХ

 

 

w_s – вологість насичення;

w_r – максимальна гігроскопічність;

НВ – найменша вологоємність;

ВВ – вологість в'янення.